製造業において、サンプルサイズを5個に設定する理由には、統計学的な背景と実務的な利便性があります。特に品質管理の現場では、サンプル数が製品のばらつきを適切に評価するための重要な要素となります。本記事では、サンプルサイズの決定に影響を与える統計学の理論や、コストと精度のバランスをどのように取るかについて詳しく解説します。
統計学は数学のスキルが必要ですが、今回の内容は数式を極限まで使わないで説明した「読み物」にしてありますので、数学が苦手な方でも安心して読むことができます！
品質マネジメントシステム普及の応援が目的のサイトです！「難解な規格を簡単に解説」をモットーに、「ちょっと相談したい」ときに頼りになるコンサルタントを目指しています！まずはお気軽にご連絡ください★
「無料で学ぶ」「有料で実践する」——皆様の目的に合わせて活用可能です！
✅ QMS・品質管理・製造ノウハウを無料で学びたい方へ
👉 本サイト「QMS学習支援サイト」を活用しましょう！「QMSについて知りたい」「品質管理の基礎を学びたい」方に最適！
✔ IATF 16949やISO 9001・VDA6.3の基礎を学ぶ
✔ 品質管理や製造ノウハウを無料で読む
✔ 実務に役立つ情報を定期的にチェック
✅ 実践的なツールやサポートが欲しい方へ
👉 姉妹サイト「QMS認証パートナー」では、実務で使える有料のサポートサービスを提供！「すぐに使える資料が欲しい」「専門家のサポートが必要」な方に最適！
✔ コンサルティングで具体的な課題を解決
✔ すぐに使える帳票や規定のサンプルを購入
✔ より実践的な学習教材でスキルアップ
皆様の目的に合わせて活用可能です！
| ・当サイトの内容は、あくまでもコンサルタントとして経験による見解です。そのため、保証するものではございません。 ・各規格の原文はありません。また、規格番号や題目なども当社の解釈です。 ・各規格については、規格公式サイトを必ず確認してください。 ・メールコンサルティングは空きあります(2025年9月現在)。この機会に「ちょっと相談」してみませんか？1質問の無料サービス期間を是非ご利用ください。 →サービスのお問い合わせはこちら |
2025年：新企画始動告知！
メールコンサルティング初回契約：初月50%以上割引★
サービス詳細はこちら
・オンラインコンサル/現地コンサルの空き状況について
【現在の空き状況：2025年9月現在】
・平日：6時間以上ご利用で月1回のみ空きあり
・夜間：19:30-21:00でご相談承ります
・土日：少々空きあります
オンライン会議システムを利用したコンサル詳細はこちら
IATF16949構築の最初の一歩に必要な実務教材やサンプル・テンプレを販売しています。「何から始めればいい？」「要求事項をどう展開する？」と悩む担当者様向けに、実務で使える知識と資料をまとめた内容です。
メールコンサルティングで簡単相談
文書作成の不安や現場とのギャップに悩む企業様には、IATF・ISO専門のメールコンサルをご用意。資料を確認し、具体的な改善アドバイスをメールでお届けします。初回相談は無料です。
この記事の目次
製造業でサンプルサイズを5個にする理由
製造業において、サンプルサイズN=5が選ばれることってよくありませんか？「検査数はN=５個ね」と言われても「なんでN=５なの？その理由なんだろう・・・？」とわからないで使っている人はかなり多いと思います。多分ほとんどの人が知らない。
理由は、統計学的にN=５個だと信頼できるからです。もう少しいうと、信頼性と効率のバランスを取るためです。
1個や3個では、ばらつきを捉えるには不十分であり、逆にサンプル数が多すぎるとコストや時間がかかります。この5個という数は、品質管理のプロセスで最低限の統計的信頼性を確保できる数として一般的に採用されているのです。
また、製品の製造工程におけるばらつきを把握するためにも、ランダムに5個のサンプルを取ることで、製品の品質を適切に管理できるからというのが結論です。
統計学に基づくサンプルサイズの決定要因
サンプルサイズの決定には、統計学的な要素が大きく関わります。
ちょっと難しい話になりますが具体的には、信頼水準、標準偏差、誤差の許容範囲がサンプル数を決定する上で重要です。
例えば、95%の信頼水準を選ぶ場合、1.96のZ値が使用されます。標準偏差が大きければ、推定誤差を小さくするためにサンプル数を増やす必要がありますが、製造業ではサンプルサイズ5個でも十分な推定精度を得ることができる場合が多いです。
統計的にバランスの取れた数がN=5であり、信頼区間を確保しながらもコストを抑えた選択と言えるつまり「絶妙なバランスがとれた数字がN=５」なんです。
ISO9001・IATF16949・VDA6.3に関するちょっとした疑問や不安。「誰かに聞けたらすぐ解決するのに…」と感じたことはありませんか？「これでいいのかな…」そんな不安を、メールで一緒に解消しませんか？小さな疑問からでも遠慮なく相談できます。
・面談不要、メールだけで完結
・初回は、1質問無料！納得してからご利用可能です
・月額プラン(サブスク形式)なら自動更新！何度でも安心相談可能！
中心極限定理とサンプル数の関係
もっと難しい話になるので、ここは興味がある人だけ読んでください（笑）。
中心極限定理は、サンプル数が十分大きくなると、どんな分布からでもサンプル平均は正規分布に近づくという理論です。この理論によって、製造業ではサンプル数N=5個が採用されています。
N=5という数は、大規模なサンプルを取ることなく、サンプルの平均が母集団の平均に近づくための最低限のサンプル数として実用的です。もちろん、製品のばらつきが大きい場合には、さらに多くのサンプルが必要になることもありますが、5個であれば中心極限定理の影響を十分に活用できるため、品質管理においても有効です。
品質管理におけるサンプルサイズの重要性
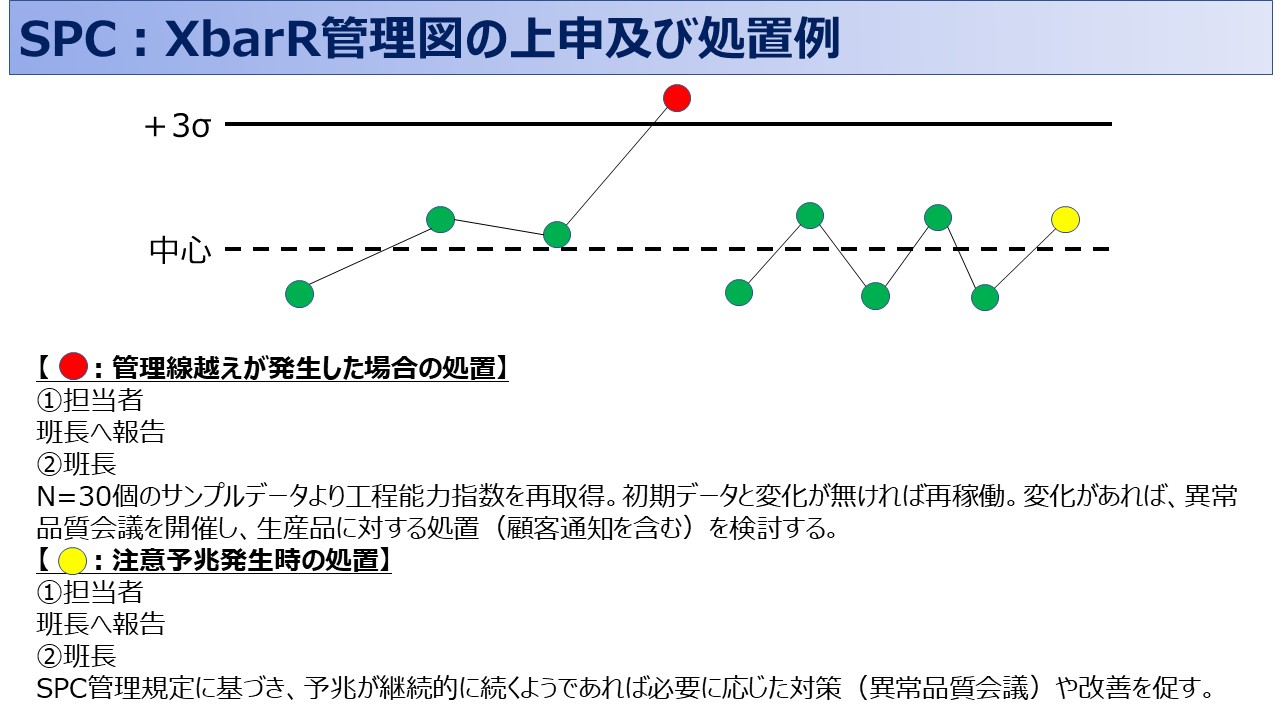
製造業において品質管理を行う際、適切なサンプルサイズの選定は欠かせません。特に統計的工程管理（SPC）や実験計画法（DOE）では、サンプル数がプロセスのばらつきや安定性をモニタリングする上で重要な要素です。
5個のサンプルをランダムに取ることで、プロセスの異常を検出する確率が高まり、品質の維持に役立ちます。サンプル数を5にすることは、コストや時間を最小限に抑えつつも、製品の安定した品質を確保するために最適な手法です。
よく「N=1やN=3の検査数ではだめですか？」と質問される方がいらっしゃるのですが、今回のご説明のように答えはNoです。皆さんも統計学的にN=5が有益な理由がお分かりいただけたと思うので、今後は社内で質問されたら是非理由を説明してあげてくださいね！
SPCに関する関連記事
N数を増やす必要がある場合
逆に上司から「〇〇工程で不良が出てきたからN数増やしてデータ解析して」とお願いされることもありますよね？
この時N=30個やN＝125個を取得要求されることもあると思いますが、これはモニタリングの用途ではなく、解析の用途になる為必要になると考えておくとわかりやすいと思います。
製品のばらつきが非常に大きい場合や、より高い精度が求められる場合には、サンプルサイズを増やす必要が出てくるからです。
一般的に、サンプル数が30個以上になると、統計学的な信頼性がさらに高まります。これにより、推定の誤差が減り、製品の品質や工程のばらつきをより正確に把握できます。しかし、製造現場でN=5が採用される理由は、コストや時間の効率を重視しながらも、必要な信頼性を保つことができるために使用されるのでN=５とされます。
サンプルサイズN=５の理由：まとめ
製造業におけるサンプルサイズN=5の設定は、統計学的な根拠と現場での効率を両立させた合理的な選択だとおわかりいただけたでしょうか。
サンプルサイズを増やすほど推定の精度が上がる一方で、コストや時間も増加します。N=5は、信頼性をある程度確保しながらも、効率的に品質管理を行うための適切なバランスが取れた数です。
ちょっと難しい話ですが中心極限定理により、5個のサンプルでも母集団の特性を正確に反映できる可能性が高く、品質管理におけるばらつきの検出やプロセスの安定性評価にも十分対応可能となります。もちろん、ばらつきの大きい製品や高い精度を求められる場合には、30個以上のサンプルが推奨されますが、製造業の現場ではN=5が実用的かつ経済的な基準として広く採用されています。
本記事を通じて、製造業でのサンプルサイズ決定の理由について理解が深まることができれば幸いです。
弊社QMS認証パートナーは、製造業に特化した品質マネジメントシステム（QMS）の認証取得からその後の維持・運用・管理まで実務経験に基づいた実用的なサポートを提供しております。初めての認証取得/取得後の課題に対しても、シンプルかつ現場で活用できる仕組みづくりを重視しています。
・教材（電子書籍）の教育教材
・規定類・帳票類のサンプルによる自力構築支援
・メールコンサルティング
最終的には「自社で回せる品質マネジメントシステム」を目指して、継続的な改善・運用が可能な体制の構築を目指します！
